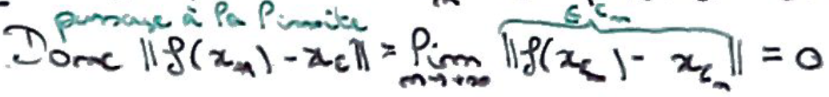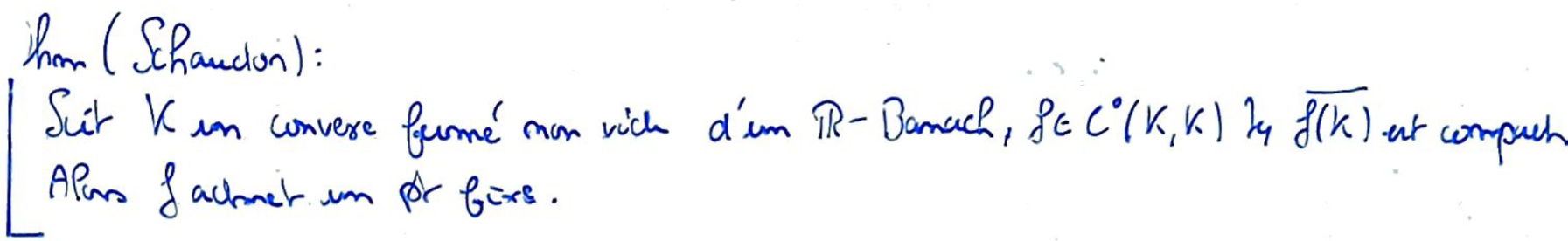
On pose l'adhérence de l'enveloppe convexe de \(f(K)\), qui est compacte en tant qu'enveloppe convexe d'un précompact.

En utilisant le fait que \(f\) est une Transformation de \(K\), on a que cette adhérence d'enveloppe convexe est dans \(K\).

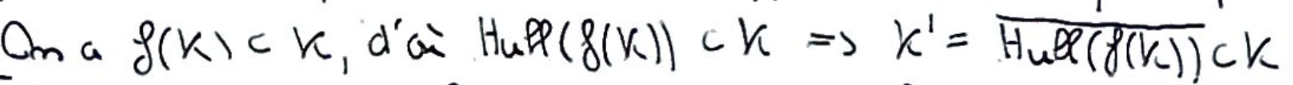
Par précompacité de \(K\), on le recouvre d'un nombre fini de boules arbitrairement petites \(\to\) on pose l'adhérence de l'enveloppe convexe de ces points et une fonction \(g_\varepsilon\) qui projette les points vers le centre de la boule du recouvrement à laquelle elle fait partie.

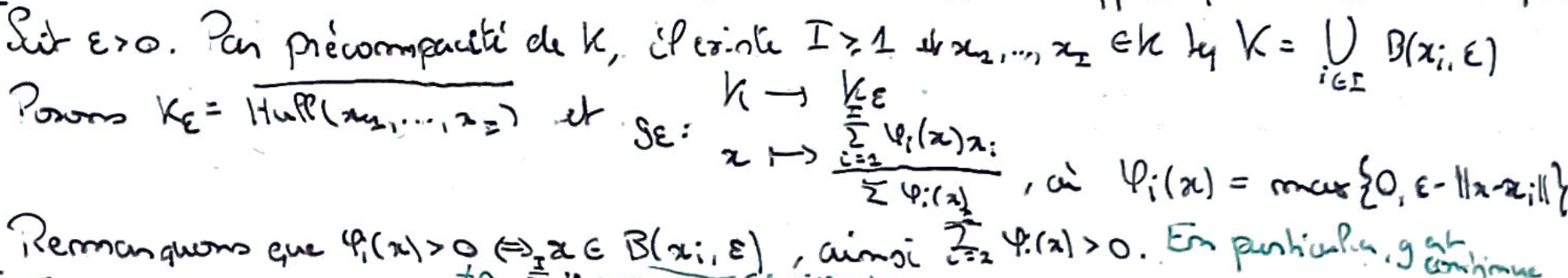
On montre que \(\lVert g_\varepsilon(x)-x\rVert\leqslant\varepsilon\) par inégalité triangulaire.

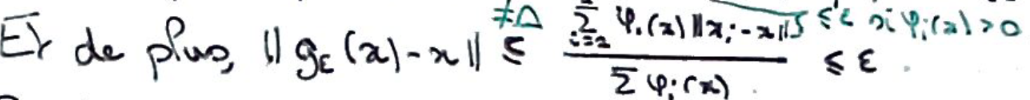
Par le Théorème du point fixe de Brouwer, \(g_\varepsilon\circ f_{\rvert K_\varepsilon}\) admet donc un point fixe.

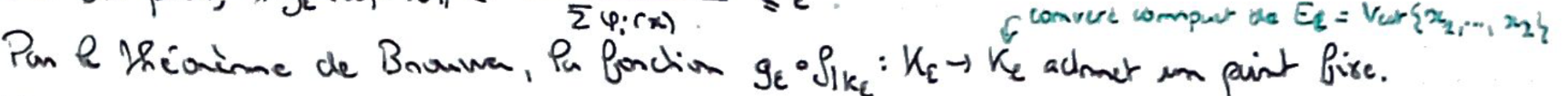
Par compacité, on peut prendre une suite de \(\varepsilon_n\) qui tend vers \(0\) et telle que \(\lVert f(x_{\varepsilon_n}-x_{\varepsilon_n})\rVert\leqslant\varepsilon_n\) via un théorème belge avec \(g_{\varepsilon_n}\circ f(x_{\varepsilon_n})\).

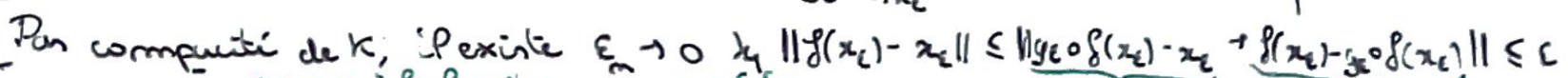
On peut passer à la limite, ce qui nous dit que le majorant tend vers \(0\) et que \(f\) admet un point fixe.